En cálculo infinitesimal, la función primitiva o antiderivada de una función f es una función F cuya derivada es f, es decir, F ′ = f.
Una condición suficiente para que una función f admita primitivas sobre un intervalo es que sea continua en dicho intervalo.
Si una función f admite una primitiva sobre un intervalo, admite una infinidad, que difieren entre sí en una constante: si F1 y F2 son dos primitivas de f, entonces existe un número real C, tal que F1 = F2 + C. A C se le conoce como constante de integración.
Como consecuencia, si F es una primitiva de una función f, el conjunto de sus primitivas es F + C. A dicho conjunto se le llama integral indefinida de f y se representa como:
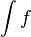 ó
ó 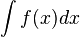
El proceso de hallar la primitiva de una función se conoce como integración indefinida y es por tanto el inverso de la derivación. Las integrales indefinidas están relacionadas con las integrales definidas a través del teorema fundamental del cálculo integral, y proporcionan un método sencillo de calcular integrales definidas de numerosas funciones.

El campo vectorial definido asignando a cada punto (x, y) un vector que tiene por pendiente
ƒ(
x) = (x
3/3)-(x
2/2)-x. Se muestran tres de las infinitas primitivas de
ƒ(
x) que se pueden obtener variando la constante de integración
C.
REGRESAR A TEMARIO