Integración directa
En ocasiones es posible aplicar la relación dada por el teorema fundamental del cálculo de forma directa. Esto es, si se conoce de antemano una función cuya derivada sea igual a f(x) (ya sea por disponer de una tabla de integrales o por haberse calculado previamente), entonces tal función es el resultado de la antiderivada.
- Ejemplo
- Calcular la integral
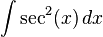 .
.
- En una tabla de derivadas se puede comprobar que la derivada de tan(x) es sec2(x). Por tanto:
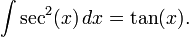
- Ejemplo
- Calcular la integral
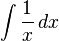 .
.
- Una fórmula estándar sobre derivadas establece que
 . De este modo, la solución del problema es
. De este modo, la solución del problema es 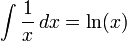 .
.
Método de integración por sustitución
El método de integración por sustitución o por cambio de variable se basa en realizar un reemplazo de variables adecuado que permita convertir el integrando en algo sencillo con una integral o antiderivada simple. En muchos casos, donde las integrales no son triviales, se puede llevar a una integral de tabla para encontrar fácilmente su primitiva. Este método realiza lo opuesto a la regla de la cadena en la derivación.
Procedimiento práctico
Supongamos que la integral a resolver es:

En la integral reemplazamos  con (u):
con (u):
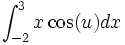 (1)
(1)
Ahora necesitamos sustituir también  para que la integral quede sólo en función de
para que la integral quede sólo en función de 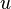 :
:
Tenemos que  por tanto derivando se obtiene
por tanto derivando se obtiene 
Se despeja  y se agrega donde corresponde en (1):
y se agrega donde corresponde en (1):

Simplificando:
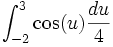
Debemos considerar si la sustitución fue útil y por tanto se llegó a una forma mejor, o por el contrario empeoró las cosas. Luego de adquirir práctica en esta operación, se puede realizar mentalmente. En este caso quedó de una manera más sencilla dado que la primitiva del coseno es el seno.
Como último paso antes de aplicar la regla de Barrow con la primitiva debemos modificar los límites de integración. Sustituimos x por el límite de integración y obtenemos uno nuevo.
En este caso, como se hizo  :
:
 (límite inferior)
(límite inferior)
 (límite superior)
(límite superior)
Luego de realizar esta operación con ambos límites la integral queda de una forma final:

Método de integración por partes
El método de integración por partes es el que resulta de aplicar el siguiente teorema:
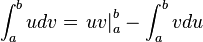 .
.
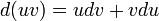
 .
.
Eligiendo adecuadamente los valores de 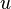 y
y  , puede simplificarse mucho la resolución de la integral.
, puede simplificarse mucho la resolución de la integral.
- Para elegir la función
 se puede usar una de las siguiente reglas mnemotécnicas:
se puede usar una de las siguiente reglas mnemotécnicas:
1) Arcoseno, arcocoseno..., Logarítmicas, Polinómicas, Exponenciales, Seno, coseno, tangente... ⇒ A L P E S.
Nota: Elegimos siempre "u" como la funcion situada más a la izquierda de la palabra ALPES.
2) Logarítmicas, Inversas, Algebráicas, Trigonométricas, Exponenciales. ⇒ L I A T E.
Nota: Elegimos siempre "u" como la funcion situada más a la izquierda de la palabra LIATE.
3) Inversas, Logarítmicas, Potenciales, Exponenciales, Trigonométricas ⇒ I L P E T
Nota: Elegimos siempre "u" como la funcion situada más a la izquierda de la palabra ILPET.
REGRESAR A TEMARIO